【Python學習】Python解決漢諾塔問題

參考文章：https://www.cnblogs.com/dmego/p/5965835.html

一句話：學程序不是目的，理解就好；寫代碼也不是必然，省事最好；拿也好，查也好，解決問題就好！

信息時代不用信息就是罪過，直接抄不加理解與應用，是不經腦子，或許其中的某一個細節就能夠用於各個問題的解決，共勉

學習一個東西總會遇到一些經典的問題，學習Python第二天嚐試看一下漢諾塔問題，還是百度，看看解題思路，純粹是重溫初中課堂，越活越回去了

 漢諾塔的圖解遞歸算法

一．起源：

　　漢諾塔（又稱河內塔）問題是源於印度一個古老傳說的益智玩具。大梵天創造世界的時候做了三根金剛石柱子，在一根柱子上從下往上按照大小順序摞著64片黃金圓盤。大梵天命令婆羅門把圓盤從下麵開始按大小順序重新擺放在另一根柱子上。並且規定，在小圓盤上不能放大圓盤，在三根柱子之間一次隻能移動一個圓盤。

二．抽象為數學問題：

　　如下圖所示，從左到右有A、B、C三根柱子，其中A柱子上麵有從小疊到大的n個圓盤，現要求將A柱子上的圓盤移到C柱子上去，期間隻有一個原則：一次隻能移到一個盤子且大盤子不能在小盤子上麵，求移動的步驟和移動的次數


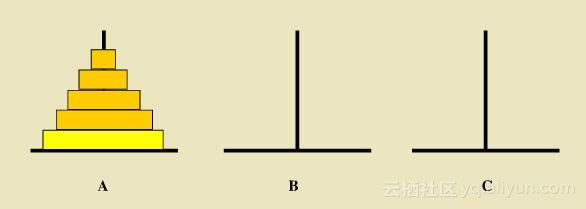
解：（1）n == 1

       第1次  1號盤  A---->C       sum = 1 次

       (2)  n == 2

       第1次  1號盤  A---->B

       第2次  2號盤  A---->C

       第3次  1號盤  B---->C        sum = 3 次

　　（3）n == 3

　　第1次  1號盤  A---->C

　　第2次  2號盤  A---->B

　　第3次  1號盤  C---->B

　　第4次  3號盤  A---->C

　　第5次  1號盤  B---->A

　　第6次  2號盤  B---->C

　　第7次  1號盤  A---->C        sum = 7 次

三．調用方法的棧機製:（特點：先進後出）

       從主線程開始調用方法（函數）進行不停的壓棧和出棧操作，函數的調用就是將函數壓如棧中，函數的結束就是函數出棧的過程，這樣就保證了方法調用的順序流，即當函數出現多層嵌套時，需要從外到內一層層把函數壓入棧中，最後棧頂的函數先執行結束（最內層的函數先執行結束）後出棧，再倒數第二層的函數執行結束出棧，到最後，第一個進棧的函數調用結束後從棧中彈出回到主線程，並且結束。

四．算法分析（遞歸算法）：

       我們在利用計算機求漢諾塔問題時，必不可少的一步是對整個實現求解進行算法分析。到目前為止，求解漢諾塔問題最簡單的算法還是同過遞歸來求，至於是什麼是遞歸，遞歸實現的機製是什麼，我們說的簡單點就是自己是一個方法或者說是函數，但是在自己這個函數裏有調用自己這個函數的語句，而這個調用怎麼才能調用結束呢？，這裏還必須有一個結束點，或者具體的說是在調用到某一次後函數能返回一個確定的值，接著倒數第二個就能返回一個確定的值，一直到第一次調用的這個函數能返回一個確定的值。

       實現這個算法可以簡單分為三個步驟：

　　　　（1）     把n-1個盤子由A 移到 B；

　　　　（2）     把第n個盤子由 A移到 C；

　　　　（3）     把n-1個盤子由B 移到 C；

從這裏入手，在加上上麵數學問題解法的分析，我們不難發現，移到的步數必定為奇數步：

　　　　（1）中間的一步是把最大的一個盤子由A移到C上去；

　　　　（2）中間一步之上可以看成把A上n-1個盤子通過借助輔助塔（C塔）移到了B上，

　　　　（3）中間一步之下可以看成把B上n-1個盤子通過借助輔助塔（A塔）移到了C上；

四、Python實現

網上很多資料，隻要理解就好，然後拿來自己用，遇到類似的回歸問題，再舉一反三

先看看JAVA實現，大學的時候看了幾本JAVA的書，後來沒怎麼用過，也就忘了

public static void hanoi(int n,char A,char B,char C)
    {
        if(n == 1)//圓盤隻有一個時，隻需將其從A塔移到C塔
            TowersOfHanoi.move(1, A, C);//將編b號為1的圓盤從A移到C
        else
        {//否則
            hanoi(n - 1, A, C, B);//遞歸，把A塔上編號1~n-1的圓盤移到B上，以C為輔助塔
            TowersOfHanoi.move(n, A, C);//把A塔上編號為n的圓盤移到C上
            hanoi(n - 1, B, A, C);//遞歸，把B塔上編號1~n-1的圓盤移到C上，以A為輔助塔
        }
    }



定義一個漢諾塔函數

def hanoi(n, A, B, C):
     if n==1:
           print(A+'->'+C)
     else:
           hanoi(n-1, A, C, B)
           print(A+'->'+C)
           hanoi(n-1, B, A, C)

hanoi(3, 'A', 'B', 'C')

函數作為參數直接調用